ملخص الدرس / الثالثة ثانوي/رياضيات/الإحصاء و الإحتمالات /الإحتمالات المتساوية على مجموعة منتهية

الملخص

الإحتمالات

عندما يكون لديك مجموعتين مع $W$ هي المجموعة الكلية و $A$ هي المجموعة الجزئية و تمثل الأعداد الزوجية و $B$ هي مجموعة جزئية من $W$

$W=\left \{ 1.2.3.4.5.6.7.8.9 \right \}$

$A=\left \{ 2.4.6.8 \right \}$

$B=\left \{ 7.8.9 \right \}$

أحسب الإحتمالات التالية : $P(A)$ و $P(B)$ و $\overline{P(A)}$ و $P(A\cup B)$ و $P(A\cap B)$

$=4/9$ عدد عناصر $W$ $/$ عدد عناصر $A$ $P(A)=$

$=3/9=1/3$ عدد عناصر $W$ $/$ عدد عناصر $B$ $P(B)=$

$\overline{P(A)}$ يمثل الإحتمال العكسي لـ $P(A)$

$\overline{P(A)}=1-P(A)=1-\frac{4}{9}=\frac{5}{9}$

بطريقة أخرى يعني مجموعة $\overline{A}$ هي عكس الأعداد الزوجية و هي الأفراد الفردية $\overline{A}=\left \{ 1.3.5.7.9 \right \}$

عدد عناصر $W$ $/$ عدد عناصر $\overline{A}$ $\overline{P(A)}=$

الآن نقوم بحساب المجموعتين $A\cap B$ و $A\cup B$ :

$A\cap B=\left \{ 8 \right \}$

$A\cup B=\left \{ 2.4.6.8.7.9 \right \}$

$=1/9$ عدد عناصر $W$ $/$ عدد عناصر $A\cap B$ $P(A\cap B)=$

$=6/9$ عدد عناصر $W$ $/$ عدد عناصر $A\cup B$ $P(A\cup B)=$

بطريقة أخرى لحساب $P(A\cap B)$ :

$P(A\cap B)=P(A)+P(B)-P(A\cup B)\\\\ P(A\cap B)=\frac{4}{9}+\frac{3}{9}-\frac{6}{9}=\frac{7-6}{9}=\frac{1}{9}$

قانون برنولي

تعريف :

نسمي تجربة برنولي كل تجربة عشوائية ذات مخرجين متعاكسين $S$ و $\overline{S}$ باحتمالين $p$ و $1-p$ على الترتيب قانون برنولي هو المتغير العشوائي حيث :

* $X=1$ إذا تحقق المخرج $S$

* $X=0$ إذا تحقق المخرج $\overline{S}$

قانةن احتمال $X$ هو

نسمي $P$ وسيط $X$

خاصية :

إذا كان المتغير العشوائي $X$ يتبع قانون برنولي بوسيط $p$ فإن الأمل الرياضياتي $E(x)$ و التباين $V(x)$ يعطيان بالعلاقتين التاليتين : $E(x)=p$ و $V(x)=p(1-p)$

برهان :

$E(x)=0\times P(x=0)+1\times P(x=1)=P\\\\ V(X)=[0-E(x)]^2p(x=0)+[1-E(x)]^2p(x=1)\\ \\=p^2(1-P)+(1-P)^2P \\\\ =P(1-P)[P+(1-P)]=P(1-P)$

1- مخطط برنولي و قانون ثنائي الحد :

بتكرار تجربة برنولي $n$ مرة (التجارب مستقلة ) نعرف مخطط برنولي

تعريف :

نقول أن متغير عشوائي $X$ يتبع قانون ثننائي الحد بالوسطين $n$ و $P$ إذا كان $X$ يأخذ كقيمة عدد مرات تحقق المخرج $S$ عند تكرار تجربة برنولي $n$ مرة . و تكتب أحيانا $X~B(n,p)$

مبرهنة :

ليكن $n$ عددا طبيعيا غير معدوم و $p$ عددا حقيقيا من المجال $[0;1]$ ,

$X$ متغير يتبع قانةن ثنائي الحد $B(n,p)$ من أجل كل عدد طبيعي $(0 \leq k \leq 1)$ لدينا :

$P(x=k)=C_n^kp^k(1-p)^{n-k};E(x)=np;V(x)=np(1-p)$

برهان : من أجل فرع معين يحوي $k$ مرة المخرج $S$ أي $(n-k)$

مرة المخرج $\overline{S}$ يكون الاحتمال $p^k(1-p)^{n-k}$ (التجارب مستقلة )

عدد الفروع من هذا النوع (أي التي تحتوي $k$ مرة $S$ )

هو $C_n^k$ ( اختيار $k$ موضع لـ $S$ من بين $n$ موضعا )

و منه $P(x=k)=C_n^kp^k(1-p)^{n-k }$

قوانين الاحتمالات المستمرة

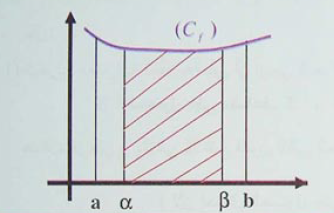
1 - الكثافة :

تعريف 1:

$f$ دالة معرفة على المجال $[a;b]$ , $(a\prec b)$

نقول أن $f$ كثافة احتمال على $[a;b]$ إذا تحقق مايلي :

(1) $f$ مستمرة على $[a;b]$ (2) $f$ موجبة على $[a;b]$ (3) $\int _a^bf(t)dt =1$

تعريف 2 :

نقول أن $X$ متغير عشوائي معرف على المجال $[a;b]$ قانون احتماله $P$ يقبل $f$ كثافة تحقق مايلي

من أجل كل عددين $\alpha$ و $\beta$ من $(\beta \geq \lpha ), [a;b]$ لدينا $p(X\in[\alpha ;\beta])=\int _a^bf(t)dt$

خواص :

من أجل كل $\alpha$ و $\beta$ ينتميان الى المجال $[a;b]$

* $p(X=\alpha )=0$

* $p(\alpha \leq X)=p(\alpha \prec X\leq \beta)=p(\alpha \prec X\prec \beta )=p(\alpha \leq X\leq \beta)$

2- قانون التوزيعات المنتضمة :

تعريف :

$f$ دالة نقول أن المتغير العشوائي $X$ يتبع قانون التوزيع المنتظم على المجال $[a;b]$ , $(a\prec b)$ إذا كانت دالة كثافة الاحتمال ثابتة على المجال $[a;b]$

ينتج من التعريف :

$\int _a^bf(t)dt =I$ و منه $\int _a^bkdt =I$ و بالتالي : $k=\frac{1}{b-a}$

أي أن من أجل كل $x$ يتمي الى $[a;b]$ يكون $f(x)=\frac{1}{b-a}$

* من أجل كل $x$ ينتمي الى $[a;b]$ لدينا : $P(X\leq x)=\frac{x-a}{b-a}$

لأن $P(X\leq x)=P(\leq a\leq X\leq x)$ أي أن $P(X\leq x)=\int _a^x\frac{dt}{b-a}$ و بالتالي $P(X\leq x)=\frac{x-a}{b-a}$

* الأمل الرياضياتي للمتغير $X$ هو $E(X)=\frac{a+b}{2}$

من التعريف , الأمل الرياضياتي لمتغير مستمر كثافته $f$ هو $E(X)=\int _a^bxf(x)dx$ أي $E(X)=\int _a^b\frac{x}{b-a}$

و بحساب بسيط نجد $E(X)=\frac{a+b}{2}$

قياس تلاؤم سلسلة مشاهدة ونموذج احتمالي

طرح الإشكال : نريد معرفة ما إذا كان حجر نرد ذي $6$ أوجه متزنا . من أجل هذا نرمي هذا الحجر $1000$ مرة و نحسب تواترات ظهور الأرقام من $1$ الى $6$ . نرمز لهذه التواترات بالرموز $f_6,f_5,f_4,f_3,f_2,f_1$ و إذا اقتربت هذه التوترات من $\frac{1}{6}$ فإن الحجر متزن .

نذكر أنه فيالسنة الثانية , أثبتنا بالمحاكاة تقارب التواترات و الاحتمالات و عليه سنحسب المسافة $d$ حيث $d ^2=\sum _i=1^6\left ( f_1-\frac{1}{6} \right )^2$ كلما كانت $d^2$ أصغر كان الحجر متزنا .

لنقم بالمحاكاة :

1- في المجدول إكسال , أدخل في الخلايا من $B_2$ الى $F_{21}$ العبارة $=Ent(6*ALE()+1$

2- في الخلية $2$ أكتب $I2:I10$ ثم عمم باستعمال الزالق على الحيز

3- في الخلية $J2$ أدخل $=I2/100$ ثم بالزالقعمم على الحيز $J2:J10$

الوجه	ع الظهور	التواتر
$1$	$170$	$0,170$
$2$	$178$	$0,178$
$3$	$168$	$0,168$
$4$	$182$	$0,182$
$5$	$146$	$0,146$
$6$	$156$	$0,156$

4- في الخلية $H13$ أكتب $\left \{ =(Somme((J2:J10)^2)) \right \}$ إذا لم تستعمل $\left \{ \right \}$ فما عليك سوى بالنقر على $CTRL=MAJ=ENTRER$ في آن واحد

- نحسب $d^2$ :

$d^2=\left \(0,17-\frac{1}{6}\right )^2+\left ( 0,168-\frac{1}{6}+ \right )^2+\left (0,182-\frac{1}{6} \right )^2+ \left ( 0,146-\frac{1}{6} \right )^2+\left ( 0,156-\frac{1}{6} \right )^2\simeq 0,00092$

هل قيمة $d^2$ المحصل عليها تجعلنا نجزم يالحكم على حجر النرد (هل هو متزن أم لا ؟ ) .و عليه ينبغي معرفة القيم الممكن للعدد $d^2$ . عندئذ نأخذ حجر متزن و نكرر التجربة (رمي الحجر $1000$ مرة ) عندة مرات .

كررنا التجربة $3000$ مرة فحصلنا على قيم $d^2$ ملخصة في مخطط بالعلبة (لاحظ الوثيقة المرفقة )

إذا كان $d^2$ أكبر من العشري التاسع من السلسلة المرجعية الملخصة أعلاه , نقول أن الفرضية "الحجر متزن " مرفوضة بمجازفة بالخطأ مقدارها $10\%$ لأن ( $10\%$ من قيم $d^2$ هي أكبر من العشري التاسع ) . في الحال العكسية نقول أن الفرضية "الحجر متزن " غير مرفوضة .

في المثال السابق لدينا : $d^2\prec d_0$ و عليه فالفرضية "الحجر متزن " غير مرفوضة .

ملاحظة :

يمكن اختيار مجازفة بالخطأ مقدارها $5\%$ و هنا نغير العتبة فنقارن $d^2$ بالعشريني التاسع عشر

القانون الأسي

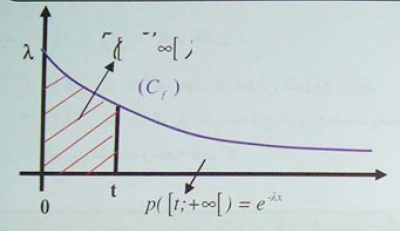
تعريف :

نقول أن المتغير العشوائي $X$ يتبع الأساسي ذي الوسيط $\lambda$ إذا كانت دالة كثافة احتماله هي الدالة $f$ المعرفة من أجل كل $x$ من المجال $[0;+\infty[$ بالعبارة $f(x)=\lambda e^{\lambda x}$

نتائج :

1)ليكن $X$ عددا من المجال $[0;+\infty[$ لدينا

البرهان :

$P(X\leq x)=\int _0^x\lambda e^{\lambda t}dt=[-e^{\lambda t}]_0^x\\\\ =-e^{-\lambdax}-e^0=1-e^{-\lambda x}$

2) الأمل الرياضاتي للمتغير $X$ هو $E(X)=\frac{1}{\lambda}$

البرهان :

$E(X)=\int_0^{+\infty}tf(t)dt=\int _0^{+\infty}\lambda t e^{-\lambda t}dt$

باستعمال المكاملة بالتجزئة :

نضع $\begin{cases} u(t)=t \\ v'(t) =\lambda e^{-\lambda t} \end{cases}$ و بالتالي $\begin{cases} u'(t)=1 \\ v(t)=-e^{-\lambda t} \end{cases}$

$E(X)=\lim_{\alpha \rightarrow +\infty}[t e^{-\lambda t}]_0^\alpha +\lim_{\alpha \rightarrow +\infty } -\frac{1}{\lambda}\left [ e^{\lambda t} \right ]_0^\alpha =\frac{1}{\lambda }$

مثال : ليكن $X$ متغير عشوائي يتبع قانةنا أسيا بوسيط $\lambda$ . عين $\lambda$ إذا علمت أن $P(X\geq 50)=\frac{2}{3}$

حل :

لدينا : $P(x\geq 50)=1-P(X\prec 50)$

و بالتالي $P(X\geq 50)=1(1-e^{-50\lambda})=e^{-50\lambda}$

نحل المعادلة $e ^{-50\lambda }=\frac{2}{3}$ نجد $\lambda=\frac{1}{50}\ln \left ( \frac{3}{2} \right )$