ملخص الدرس / الثالثة ثانوي/رياضيات/الدوال العددية/الدالة اللوغارتمية النيبيرية تعاريف و خواص
تعريف
نسمي الدالة اللوغاريتمية النيبيرية الدالة التي نرمز إليها بالرمز و التي ترفق بكل عدد حقيقي
من
العدد الحقيقي
.
نتائج أولية :
- من أجل من
و من أجل كل
من
،
يعني
.
- من أجل من
،
.
- من أجل من
،
- بما أن فإن
و بما أن
فإن
.
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :
مجموعة التعريف
دالة كيفية و
:
الخواص الجبرية
من أجل عددين حقيقيين و
من
:
من أجل كل عدد حقيقي و من أجل عدد حصيص نسبي
.
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :
الفيديو الثاني :
قواعد الحساب
1- العلاقة بين و
مثل العلاقة بين
و" التربيع "معناه
2- تكافئ
3- تكافئ
4- من أجل العددان الحثقيقيان و
الموجبن تماما و العدد الطبيعي
يكون
* *
5- إذا كان و
فإن
* *
6- و بصفة عامة
7- تعيين : إذا كانت
فردية فإن
و إذا كانت زوجية فإن
و بصفة عامة : إذا كانت
فردية فإن
و إذا كانت زوجية فإن
8- و
ما يجب معرفته و فهمه لحل المعادلات و المتراجحات
* يكافئ
* يكافئ
* يكافئ
* يكافئ
* يكافئ
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :
دراسة إشارة بعض العبارات
في كل ممايلي ترمز الى أعداد حقيقية
1- دراسة إشارة العبارة حيث
لراسة إشارة العبارة على مجموعة تعريفها نبحث عن القيمة التي تعدمها و لتكن
ثم نحدد إشارتها كما في الجدول التالي :
| |
الحل |
| |
|
2- دراسة إشارة العبارة حيث
:
لدراسة إشارة العبارة على
نقوم بمايلي :
نضع فتصبح العبارة
ونعين قيم
التي تعدمها (إن وجدت ) ثم نستنتج قيم
و في الأخير نشكل جدولا فيه إشارة العبارة مستخدمين القواعد المعروفة لإشارة كثيرات الحدود من الدرجة الثانية
3- دراسة إشارة العبارة حيث
:
إشارة من إشارة
داخل مجموعة التعريف
قوانين الإشتقاق
* إذا كان لدينا فإن
و بصفة عامة
فإن
* إذا كان لدينا فإن
و بصفة عامة
فإن
* إذا كان لدينا فإن
* إذا كان لدينا فإن
* إذا كان لدينا فإن
دالة اللوغاريتم النيبيري
تعريف :
دالة اللوغاريتم النيبيري هي الدالة الاصلية للدالة : على المجال
و التي تنعدم في 1 و يرمز لها بالرمز :
خواص :
(e أساس اللوغاريتم النيبيري )
- من أجل كل x من المجال و من أجل كل y من المجال
لدينا:
معناة
معناه
- من أجل كل x من المجال و من أجل كل y من
لدينا :
معناه :
- من أجل كل من
لدينا :
- إذا كان n عددا طبيعيا زوجيا فإن :
مجموعة التعريف :
- الدالة معرفة إذا كان
- الدالة معرفة إذا كان
النهايات :
الاستمرارية :
- الدالة مستمرة على المجال
- إذا كانت u دالة مستمرة و متزايدة تماما على مجال فإن الدالة
مستمرة على المجال
الاشتقاقية :
- الدالة قابلة للاشتقاق على المجال
- من أجل كل x من المجال لدينا :
- إذا كانت u دالة متزايدة تماما و قابلة للاشتقاق على مجال فإن الدالة
قابلة للاشتقاق على المجال
- من أجل كل x من المجال لدينا :
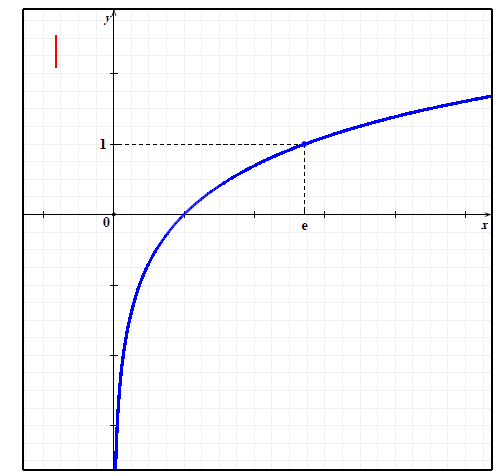
التمثيل البياني : (لاحظ الشكل 1)