ملخص الدرس / الثالثة ثانوي/رياضيات/الدوال العددية/الإشتقاقية 1

الملخص

تعريف

$f$ دالة عددية قابلة للإشتقاق على المجال المفتوح $\left ] a,b \right [$ نسمي الدالة التي ترفق بكل عدد حقيقي $x_{0}$ من المجال $\left ] a,b \right [$ العدد المشتق ${f}'\left ( x_{0} \right )$

الدالة المشتقة الأولى للدالة $f$ نرمز إليه بالرمز ${f}'$ .

مثال :

$f\left ( x \right )=x^{3}$

$f$ قابلة للإشتقاق على $\mathbb{R}$ من أجل كل عدد حقيقي $x_{0}$ العدد المشتق ${f}'\left ( x_{0} \right )$ هو $3x_{0}^{2}$ إذن : ${f}'(x)=3x^{2}$

العدد المشتق-الدالة المشتقة

تعريف :

$f$ دالة معرفة على المجال $I$ من $\mathbb{R}$ , $a$ و $a+h$ عددان حقيقيان من $I$ مع $h\neq0$ .

نقول أن $f$ تقبل الإشتقاق عند $a$ إذا قبلت النسبة $\frac{f\left ( a+h \right )-f\left ( a \right )}{h}$ ، نهاية محدودة لما يؤول $h$ إلى $0$ .تسمى هذه النهاية

العدد المشتق للدالة $f$ عند $a$ و نرمز لها بالرمز ${f}'(a)$ .

ملاحظة :

يوضع : $x=a+h$

لدينا : $\lim_{h\rightarrow 0}\frac{f\left ( a+h \right )-f\left ( a \right )}{h}={f}'\left ( a \right )$

أو : $\lim_{x\rightarrow 0}\frac{f\left ( x \right )-f\left ( a \right )}{x-a}={f}'\left ( a \right )$

المشتقات و العمليات على الدوال

ملاحظات	${f}'\left ( x \right )$ الدالة	$f(x)$ الدالة
ثابت حقيقي $a$	$x \mapsto 0$	$x \mapsto a$
$n\geq 2;n\in \mathbb{N}$	$x\mapsto nx^{n-1}$	$x \mapsto x^n$
$x\in \mathbb{R}^{\ast }$	$x \mapsto -\frac{1}{x^{2}}$	$x \mapsto \frac{1}{x}$
$x\in \left ] 0;+\infty \right [$	$x \mapsto \frac{1}{2\sqrt{x}}$	$x \mapsto \sqrt{x}$
$x\in \mathbb{R}$	$x \mapsto \cos x$	$x \mapsto \sin x$
$x\in \mathbb{R}$	$x \mapsto - \sin x$	$x \mapsto \cos x$
$b\in \mathbb{R};a\in \mathbb{R}^{\ast }$ $I$ دالة قابلة للإشتقاق على $U$	$x \mapsto a {U}'\left ( ax+b \right )$	$x \mapsto U\left ( ax+b \right )$
$I$ و $U$ دالين قابلتين للإشتقاق على $V$	$x \mapsto {U}'+{V}'$	$x \mapsto U+V$
$I$ و $U$ دالين قابلتين للإشتقاق على $V$	$x \mapsto V{U}'\times U{V}'$	$x \mapsto U\times V$
$I$ و $U$ دالين قابلتين للإشتقاق على $V$ $V\neq 0$ و	$x \mapsto \frac{{U}'V-U{V}'}{V^{2}}$	$x \mapsto \frac{U}{V}$
$n\geq 2;n\in \mathbb{N}$	$x \mapsto n{U}'U^{n-1}$	$x \mapsto \left [ U\left ( x \right ) \right ]^{n}$
$U> 0$	$x \mapsto \frac{{U}'}{2\sqrt{U}}$	$x \mapsto \sqrt{U\left ( x \right )}$

التفسير الهندسي للعدد المشتق

إذا كانت $f$ قابلة للإشتقاق من اليسار عند $x_{0}$ فإن المنحنى $\left ( C_{f} \right )$ يقبل في النقطة $A\left ( x_{0};f\left ( x_{0} \right ) \right )$ نصفي مماس في هذه الحالة النقطة $x_{0}$

تدعى نقطة زاوية معناه :

$\lim_{\overset{>}{x\rightarrow x_{0}}}\left [ \frac{f\left ( x \right )-f\left ( x_{0} \right )} {x-x_{0}} \right ]\neq \lim_{\overset{<}{x\rightarrow x_{0}}}\left [ \frac{f\left ( x \right )-f\left ( x_{0} \right )} {x-x_{0}} \right ]$

مماس منحنى الدالة

إذا قبلت الدالة $f$ للإشتقاق عند $x_{0}$ فإن المنحنى $\left ( C_{f} \right )$ يقبل في النقطة $A\left ( x_{0};f\left ( x_{0} \right ) \right )$ مماسا معامل توجيهه العدد ${f}'\left ( x_{0} \right )$

و تكون معادلة المماس : $y={f}'\left ( x_{0} \right )\left ( x-x_{0} \right )+f\left ( x_{0} \right )$

للمزيد من التفاصيل اليك الفيديوهات التالية :

الفيديو الأول :

قابلية الاشتقاق في عدد

- نقول إن دالة $f$ قابلة للاشتقاق في العدد $x_0$ إذا كانت :

$\lim _{x\rightarrow x_0 }\frac{f(x)-f(x_0)}{x-x_0}=l$

هذه النهاية تسمى العدد المشتق للدالة في و يرمز له بالرمز : $f'(x_0)$

معادلة المماس لمنحنى الدالة

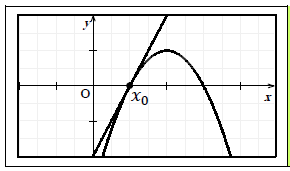
لتكن $f$ دالة قابلة للاشتقاق في $x_0$

معادلة المماس لمنحتى الدالة $f$ في النقطة التي فاصلتها $x_0$ هي : $y=f'(x_0)(x-x_0)+f(x_0)$

ملاحظة :

الدالة $u$ المعرفة على $\mathbb{R}$ كمايلي : $u(x)=f'(x_0)(x-x_0)+f(x_0)$

تسمى الدالة التآلفية المماسة لمنحنى الدالة $f$ في النقطة التي قاصلتها $x_0$ و هي تقريب للدالة $f$ بجوار $x_0$

قابلية الاشتقاق على اليمين -قابلية الاشتقاق على اليسار

- نقول إن الدالة $f$ قابلة للاشتقاق على اليمين في $x_0$ إذا كانت :

$\lim _{x\overset{>}{\rightarrow}x_0}=\frac{f(x)-f(x_0)}{x-x_0}=l_1$

هذه النهاية تسمى العدد المشتق للدالة $f$ على يمين $x_0$

- نقول إن الدالة $f$ قابلة للاشتقلق على اليسار في $x_0$ إذا كانت :

$\lim _{x\overset{<}{\rightarrow}x_0}=\frac{f(x)-f(x_0)}{x-x_0}=l_2$

هذه النهاية تسمى العدد المشتق للدالة $f$ على يسار $x_0$

ملاحظة :

تكون دالة $f$ قابلة للاشتقاق في $x_0$ إذا كانت $f$ قابلة للاشتقاق على اليمين في $x_0$ و على اليسار في $x_0$ و :

$\lim _{x\overset{>}{\rightarrow}x_0}=\frac{f(x)-f(x_0)}{x-x_0}=\lim _{x\overset{<}{\rightarrow}x_0}=\frac{f(x)-f(x_0)}{x-x_0}=l$

الاشتقاق و الاستمرارية

إذا كانت $f$ دالة قابلة للاشتقاق في العدد $x_0$

فإن : $f$ دالة مستمرة في العدد $x_0$

جدول مشتقات بعض الدوال المألوفة

$f(x)$	$f'(x)$
$k/k\in \mathbb{R}$	0
x	1
$\frac{1}{x}$	$\frac{-1}{x^2}$
$x^r/r\in \mathbb{Q}^\ast -\left \{ 1 \right \}$	$rx^{r-1}$
$\sqrt x$	$\frac{1}{2\sqrt x}$

العمليات على الدوال المشتقة

$f(x)$	$f'(x)$
$(ku)/k\in \mathbb{R}$	$(ku)'=k(u)'$
$(u-v)$	$(u-v)'=u'-v'$
$(u+v)$	$(u+v)'=u'+v'$
$(u\times v)$	$(u\times v)'=u'\times v+u\times v'$
$(u^n)$	$(u^n)'=nu^n\times u^{n-1}$
$\left ( \frac{u}{v} \right )$	$\left ( \frac{u}{v} \right )'=\frac{u'\times v- u\times v'}{v^2}$
$\left ( \frac{1}{v} \right )$	$\left ( \frac{1}{v} \right )'=\frac{-v'}{v^2}$

مشتق مركب دالتين

$(u\circ v)'=[u'\circ v]\times v'$

مشتق الدالة الجذر

$(\sqrt u)'=\frac{u'}{2\sqrt u}$

الاشتقاق و اتجاه تغير دالة

لتكن $f$ دالة قابلة للاشتقاق على المجال $I$ .

اتجاه تغي الدالة $f$	إشارة $f'(x)$
$I$ متناقصة على المجال $f$	$f'(x)\leq 0$
$I$ متزايدة على المجال $f$	$f'(x)\geq 0$
$I$ ثابتة على المجال $f$	$f'(x)=0$

الاشتقاق و التفسير الهندسي

التفسير الهندسي	قابلية الاشتقاق	النهاية
المنحنى الممثل للدالة $f$ يقبل مماسا في النقطة $A(x_0,f(x_0))$ a معامل توجيهه	$x_0$ قابلة للاشتقاق في $f$	$\lim _{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}=a\\ (a\neq0)$	1
$A(x_0;f(x_0))$ المنحنى الممثل للدالة $f$ يقبل مماسا أفقيا في النقطة	$x_0$ قابلة للاشتقاق في $f$	$\lim_{x\rightarrow x_0}\frac{f(x)f(x_0)}{x-x_0}=0$	2
المنحنى الممثل للدالة $f$ يقبل نصف مماس في النقطة $A(x_ç0;f(x_0))$ $a$ على اليمين معامل توجيهه حامله	$x_0$ قابلة للاشتقاق على يمين $f$	$\lim_{x\overset{>}{\rightarrow}x_0}\frac{f(x)-f(x_0)}{x-x0}=a\\ (a\neq 0)$	3
المنحنى الممثل للدالة $f$ يقبل نصف مماس افقي على اليمين في $A(x_0;f(x_0))$ النقطة	$x_0$ قابلة للاشتقاق على يمين $f$	$\lim_{x\overset{>}{\rightarrow}x_0}\frac{f(x)-f(x_0)}{x-x0}=0$	4
المنحنى الممثل للدالة $f$ يقبل نصف مماس عمودي على اليمين في النقطة $A(x_0;f(x_0))$ موجه نحو الاسفل	$x_0$ غير قابلة للاشتقاق على يمين $f$	$\lim_{x\overset{>}{\rightarrow}x_0}\frac{f(x)-f(x_0)}{x-x0}=-\infty$	5
المنحنى الممثل للدالة $f$ يقبل نصف مماس عمودي على اليمين في النقطة $A(x_0;f(x_0))$ موجه نحو الاعلى	$x_0$ غير قابلة للاشتقاق على يمين $f$	$\lim_{x\overset{>}{\rightarrow}x_0}\frac{f(x)-f(x_0)}{x-x0}=+\infty$	6
المنحنى الممثل للدالة $f$ يقبل نصف مماس في النقطة $A(x_0;f(x_0))$ على اليسار معامل توجيه حامله	$x_0$ قابلة للاشتقاق على يسار $f$	$\lim_{x\overset{<}{\rightarrow}x_0}\frac{f(x)-f(x_0)}{x-x0}=a\\(a\neq 0)$	7
المنحنى الممثل للدالة $f$ يقبل نصفر مماس افقي على اليسار في $A(x_0;f(x_0))$ النقطة	$x_0$ قابلة للاشتقاق على يسار $f$	$\lim_{x\overset{<}{\rightarrow}x_0}\frac{f(x)-f(x_0)}{x-x0}=0$	8
المنحتى الممثل للدالة $f$ يقبل نصف مماس عمودي على اليسار في النقطة $A(x_0;f(x_0))$ موجه نحو الاعلى	$x_0$ غير قابلة للاشتقاق على يسار $f$	$\lim_{x\overset{<}{\rightarrow}x_0}\frac{f(x)-f(x_0)}{x-x0}=-\infty$	9
المنحنى الممثل للدالة $f$ يقبل نصف مماس عمودي على اليسار في النقطة $A(x_0;f(x_0))$ موجه نحو الاسفل	$x_0$ غير للاشتقاق على يسار $f$	$\lim_{x\overset{<}{\rightarrow}x_0}\frac{f(x)-f(x_0)}{x-x0}=+\infty$	10

التفسير البياني

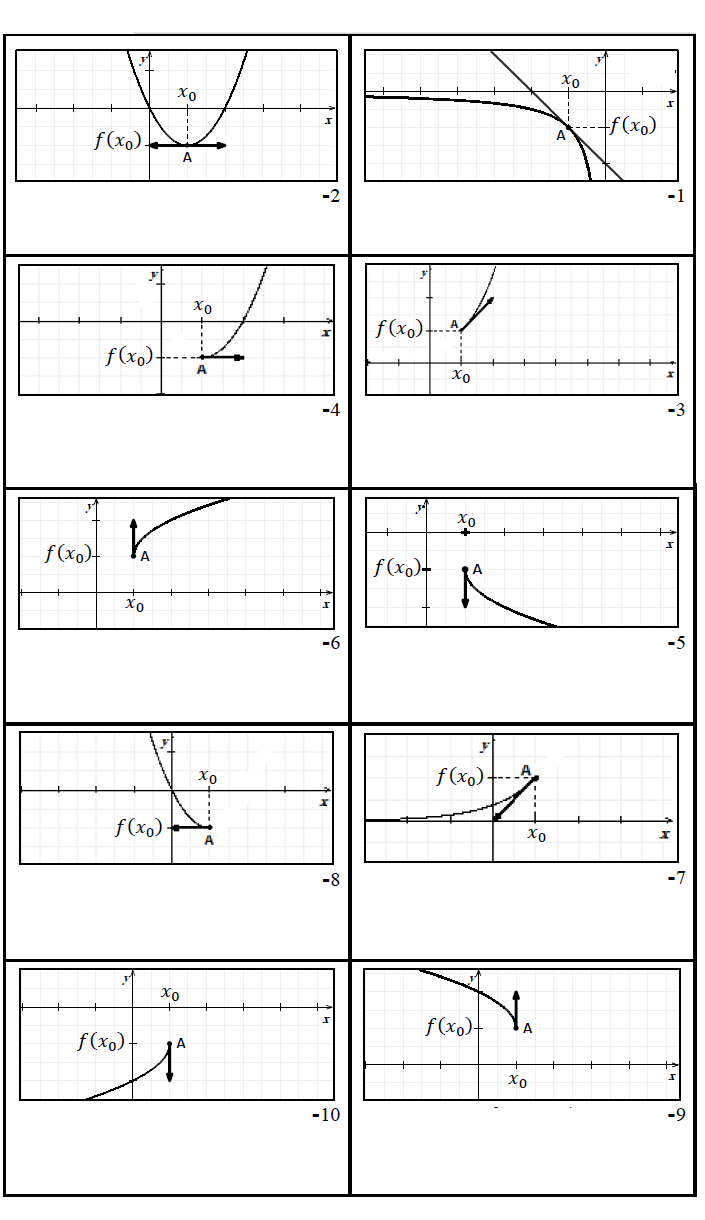
2- المنحنى الممثل للدالة $f$ يفبل ماسا أفقيا في النقطة $A(x_0;f(x_0))$	1- المنحمى الممثل للدالة $f$ يقبل مماسا في النقطة $A(x_0;f(x_0))$ معامل توجيهه $a$
4- المنحنى الممثل للدالة $f$ يقبل نصف مماس أفقي على اليمين في النقطة $A(x_0;f(x_0))$	3- المنحنى الممثل للدالة $f$ يقبل نصف مماس في المقطة $A(x_0;f(x_0))$ على اليمين معامل توجيه حامله $a$
6- المنحنى الممثل للدالة $f$ يقبل نصف مماس عمودي على اليمين في النقطة موجه نحو الأعلى $A(x_0;f(x_0))$	5- المنحنة الممثل للدالة $f$ يقبل نصف مماس عمودي على اليمين في النقطة $A(x_0;f(x_0))$ موجه نحو الاسفل
8- المنحنى الممثل للدالة $f$ يقبل نصف مماس افقي على اليسار في النقطة $A(x_0;f(x_0))$	7- المنحنى الممثل للدالة $f$ يقبل نصف مماس فب المقطة $A(x_0;f(x_0))$ على اليسار معامل توجيه حامله a
10- المنحنى الممثل للدالة $f$ يقبل نصف مماس عمودي على اليسار في النقطة $A(x_0;f(x_0))$ موجه نحو الاسفل	9- المنحنى الممثل للدالة $f$ يقبل نصف مماس عمودي على اليسار في النقطة $A(x_0;f(x_0))$ موجه نحوالاعلى

نهايات تتعلق بالاشتقاقية

الملاحظات

التفسير الهندسي

النهاية

النهاية تعني ان الدالة $f$ تقبل الاشتقاق عند القيمة $x_{0}$

المنحنى $(Cf)$ يقبل عند النقطة ذات الفاصلة $x_{0}$ -مماسا معامل توجيههه $l$

$\lim_{h\rightarrow 0}\frac{f(x_{0}+h)-f(x_{0})}{h}=l$ او $\lim_{x\rightarrow x_{0}}\frac{f(x)-f(x_{0})}{x-x_{0}}=l$ $l\epsilon R$

النهاية تعنى ان الدالة $f$ لا تقبل الاشتقاق عند القيمة $x_{0}$

لاحظ هنا ان النقطة ذات الفاصلة $x_{0}$ نقطة انعطاف ل $(Cf)$

المنحنى $(Cf)$ يقبل عند النقطة ذات الفاصلة $x_{0}$ مماسا يوازي محور التراتيب

$\lim_{x\rightarrow x_{0}}\frac{f(x)-f(x_{0})}{x-x_{0}}=-\infty$ او $\lim_{X\rightarrow X_{0}}\frac{f(x)-fx_{0}}{x-x_{0}}=+\infty$

نهايات تتعلق بالدوال $f$ التى تحقق $f(0)=0$ :

الملاحظات	التفسير الهندسي	النهاية
النهاية تعنى ان الدالة $f$ تقبل الاشتقاق عند 0	االمنحنى $(Cf)$ يقبل عند المبدا مماسا معامل توجيهه $l$	; $\lim_{x\rightarrow 0}\frac{f(x)}{x}=l$ $l\epsilon R$
النهاية تعنى ان الدالة $f$ لا تقبل الاشتقاق عند 0 *لاحظ ا هنا المبدا نقطة انعطاف ل $(Cf)$	المنحنى $(Cf)$ يقبل عند المبدا مماسا يوازي محور التراتيب	$\lim_{x\rightarrow 0}\frac{f(x)}{x}=+\infty$ او $\lim_{x\rightarrow 0}\frac{f(x)}{x}=-\infty$
النهاية تعني ان الدالة $f$ تقبل الاشتقاق عند 0 من اليمين .	$(Cf)$ يقبل عند المبدا نصف مماس ( من اليمبن) معامل توجيهه $l$	$\lim_{x\overset{> }{\rightarrow}0}\frac{f(x)}{x}=l$ $l\epsilon R$
النهاية تعني ان الدالة $f$ تقبل الاشتقاق عند 0 من اليسار	$(Cf)$ يقبل عند المبدا نصف مماس (من اليسار) معامل توجيهه $l$	$\lim_{x\overset{< }{\rightarrow}0}\frac{f(x)}{x}=l$ $l\epsilon R$
النهاية تعني ان الدالة $f$ لا تقبل الاشتقاق عند 0 من اليمين	$(Cf)$ يقبل عند المبدا نصف مماس يوازي محور التراتيب	$\lim_{x\overset{> }{\rightarrow}0}\frac{f(x)}{x}=+\infty$ او $\lim_{x\overset{> }{\rightarrow}0}\frac{f(x)}{x}=-\infty$
النهاية تعني ان الدالة $f$ لا تقبل الاشتقاق عند 0 من اليسار	$(Cf)$ يقبل عند المبدا نصف مماس يوازي محور التراتيب	$\lim_{x\overset{< }{\rightarrow}0}\frac{f(x)}{x}=+\infty$ او $\lim_{x\overset{< }{\rightarrow}0}\frac{f(x)}{x}=-\infty$