ملخص الدرس / الثآنية ثانوي/رياضيات/الجبر و التحليل/الدوال

الملخص

من الأستاذ(ة) عقيلة طايبي

الدالة و تمثيلها البياني

الدالة و تمثيلها البياني :

مفهوم الدالة :

$D_{f}$ مجال من $R$ ، الدالة $f$ هي علاقة ترفق بكل سابقة $x$ من المجال $D_{f}$ صورة واحدة فقط $y$ نرمز لها بــ $f(x)$

الصورة و السابقة :

اذا كان $x$ عنصرا من $D_{f}$ ، نسمي العدد الحقيقي $f(x)$ صورة $x$ بالدالة $f$ و نسمي $x$ سابقة $f(x)$ بالدالة $f$

ترميز و تعابير :

- يرمز عادة للدالة بالأحرف : $.....h,g,f$

- للتعبير عن الدالة نكتب :

$f: D \rightarrow R$

$x\rightarrow f(x)$

و نقرأ الدالة $f$ من $D$ في $R$ و التي ترفق بكل عنصر $x$ من $D$ العنصر $f(x)$ من $R$ . أي أنه لايجاد $y$ نحسب $f(x)$

تنبيه :

حذاري من الخلط بين $f$ رمز الدالة و $f(x)$ الذي يعبر عن $y$ صورة العدد الحقيقي $x$ بواسطة الدالة $f$

الدوال المرجعية :

1- الدالة التآلفية : $ax+b$ 6 - الدالة قيمة مطلقة : $\left | x \right |$

2- الدالة مربع : $x^{2}$ 7 - الدالة جب : $sinx$

3- الدالة مكعب : $x^{3}$ 8 - الدالة جب تمام : $cosx$

4- الدالة مقلوب : $1/x$ 9 - الدالة ظل : $tanx$

5- الدالة جذر التربيع : $\sqrt{x}$ 10 - الدالة ظل تمام : $cotanx$

التمثيل البياني لدالة :

$f$ دالة و $D_{f}$ مجال تعريفها ‏ التمثيل البياني للدالة $f$ معلم $(O,I,J)$ للمستوي هو مجموعة النقط $M(x,y)$ ! حيث :

$x\in D_{f}$ و $y=f(x)$ اذا رمزنا الى منحني الدالة $f$ بالرمز $(C_{f})$ فان $y=f(x)$ هي معادلة $(C_{f})$ في المعلم $(O,I,J)$ أنظر الشكل المقابل

نتيجة :

نقول أن النقطة $A (x_{A},y_{A})$ تنتمي الى المنحنى $(C_{f})$ اذا كان $x_{A}\in D_{f}$ و $y_{A}=f(x_{A})$

الفاصلة و الترتيبة :

$f$ دالة و $(C)$ تمثيلها البياني في المعلم $(0, \vec{I} , \vec{J})$ .

- فاصلة نقطة من المنحني $(C)$ هي محلها على المحور الأفقي $(xx')$ للمعلم $(0, \vec{I} , \vec{J})$ و قيمتها هي السابقة $x$ .

. ترتيبة نقطةمن المنحني $(C)$ هي محلها على المحور العمودي $(yy')$ للمعلم $(0, \vec{I} , \vec{J})$ و قيمتها هي الصورة $y$ .

مجال تعريف دالة

مجال التعريف :

مجال التعريف $D_{f}$ لدالة $f$ مجموعة بدئها $E$ و مجموعة وصولها $I$ هو مجموعة السوابق من $E$ التي تمتلك صورا بالدائة $f$ بعبارة أخرى مجموعتة العناصر $x$ التي من أجلها تكون $f(x)$ موجودة.

نتيجة مباشرة :

تكون الدالة $f$ غير معرفة في المجال الذي لا يمكن فيه ايجاد صورة $f(x)$ للسابقة $x$ بواسطة الدالة $f$ .

التفسير الهندسي :

$f$ دالة و $(C_{f})$ تمثيلها البياني ، مجال التعريف $D_{f}$ للدالة $f$ هوالمجال الذي يكون فيه لكل فاصلة $x$ ترتيبة $y$ (واحدة فقط ) بواسطة $(C_{f})$ . أي هو مجموعة الفواصل التي يمكن ايجاد ترتيبة (واحدة فقط) لها بالاسقاط على المنحني $(C_{f})$

انظر الشكل المقابل

طريقة : مجال التعريف بيانيا :

بيانيا مجموعة تعريف دالة هو اتحاد مجالات الفواصل التي لها صورة بواسطة المنحني الممثل للدالة .

تعميم الشروط :

* عبارة جبرية و $f$ دالة مجال تعريفها $D_{f}$

- تكون الدالة الناطقة معرفة اذا كان المقام غير معدوم : اذا كانت $f(x)= 1/*$ فان $D_{f} = \left \{ x\in R : *\neq 0 \right \}$

- تكون الدالة الصماء معرفة اذا كان ما تحت الجذر أكبر من أو يساوي الصفر : اذا كانت $f(x)= \sqrt{*}$ فان $D_{f} = \left \{ x\in R : *\geq 0 \right \}$

- الدوال التي تكتب من الشكل $ax^{n}+bx^{n-1} + cx^{n-2}$ مثل الدالة التآلفية و الدالة مربع و مكعب معرفة على $R$ أي $D_{f}= ] - \infty ,+\infty \left [$

- تكون دالة القيمة المطلقة معرفة على المجال الذي يكون ما بداخل القيمة المطلقة معرف عليه . اذا كانت $f(x) = \left | * \right |$ فان $D_{f}= D_{*}$

- تكون دالة الجب معرفة على المجال الذي يكون ما بداخل القوسين معرف عليه . اذا كانت $f(x)= sin(*)$ فان $D_{f}= D_{*}$

- تكون دالة الجب تمام معرفة على المجال الذي يكون ما بداخل القوسين معرف عليه . اذا كانت $f(x)= cos(*)$ فان $D_{f}= D_{*}$

- تكون الدالة ظل معرفة على المجال الذي يكون ما بداخل القوسين يختلف عن $\pi /2+k\pi$ . اذا كانت $f(x)=tan(*)$ فان $D_{f} = \left \{ x\in R : *\neq\frac{\pi}{2} +k\pi\right \}$

- تكون الدالة ظل تمام معرفة على المجال الذي يكون ما بداخل القوسين يختلف عن $k\pi$ . اذا كانت $f(x)=cotan(*)$ فان $D_{f} = \left \{ x\in R : *\neq k\pi \right \}$

طريقة : مجال التعريف حسابيا :

- اذا كانت الدالة ناطقة و كان مقامها جذرا يكفي أن يكونٍ ما بداخل الجذر أكبر تماما من الصفر.

- اذا تطابق أو تكرر شرط نأخذه مرة واحدة فقط.

- حسابيا؛ مجمومة تعريف دالة هو تقاطع مجمومة عناصر كل شرط اذا تظمن شرط تعريفها عدة شروط .

تنبيه ! حذاري من التبسيط :

يجب ايجاد مجموعة تعريف الدالةّ بالشكل الذي ورد به في النص دون تبسيطها حتى وان كان ذالك ممكنا .

ملاحظة :

القيمة المطلقة لا تفرض شروط في مجال التعريف لكن احترام خواصها أثناء العمليات الحسابية.

اتجاه تغير دالة

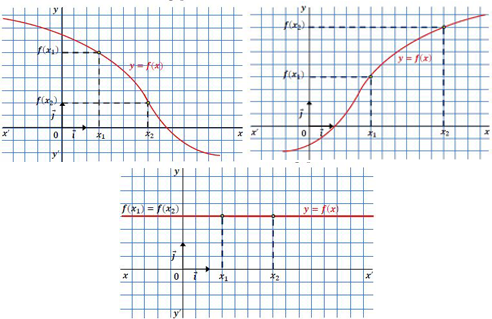
الدالة متزايدة :

لتكن $f$ دالة عددية معرفة على $D_{f}$ و $I$ مجال من $D_{f}$ و ليكن $x_{1}$ و $x_{2}$ عددان حقيقيان ينتميان الى المجال ‏ $I$

* نقول عن الدالة أنها متزايدة على $I$ اذا كان : مهما يكن $x_{2}\geq x_{1}$ فان $f(x_{2})\geq f(x_{1})$

* نقول عن الدالة أنها متزايدة تماما على $I$ اذا كان : مهما يكن $x_{2}> x_{1}$ فان $f(x_{2})> f(x_{1})$

Chargement en cours, Veuillez patientez...

الدالة متناقصة :

لتكن $f$ دالة عددية معرفة على $D_{f}$ و $I$ مجال من $D_{f}$ و ليكن $x_{1}$ و $x_{2}$ عددان حقيقيان ينتميان الى المجال ‏ $I$

* نقول عن الدالة أنها متناقصة على $I$ اذا كان : مهما يكن $x_{2}\geq x_{1}$ فان $f(x_{2}) \leq f(x_{1})$

* نقول عن الدالة أنها متناقصة تماما على $I$ اذا كان : مهما يكن $x_{2}> x_{1}$ فان $f(x_{2})< f(x_{1})$

Chargement en cours, Veuillez patientez...

رتابة دالة :

* نقول عن الدالة $f$ أنها رتيبة اذا كانت متزايدة أو متناقصة

* نقول عن الدالة $f$ أنها رتيبة تماما اذا كانت متزايدة تماما أو متناقصة تماما .

الدالة الثابتة :

لتكن $f$ دالة عددية معرفة على $D_{f}$ و $I$ مجال من $D_{f}$ و ليكن $x_{1}$ و $x_{2}$ عددان حقيقيان ينتميان الى المجال ‏ $I$

* نقول عن الدالة أنها متناقصة على $I$ اذا كان : مهما يكن $x_{2}\geq x_{1}$ فان $f(x_{2}) = f(x_{1})$

Chargement en cours, Veuillez patientez...

تنبيه ! تغير ام اشارة :

حذاري من الخلط بين الدالة المتناقصة و السالبة ، و بين الدالة المتزايدة و الموجبة ، فالدالة يمكن أن تكون متزايدة و سالبة في نفس الوقت أي أن تكون $f(x_{2})\geq f(x_{1})< 0$ أو متناقصة و موجبة في نفس الوقت أي $f(x_{2})\leq f(x_{1})> 0$

شفعية و دورية دالة

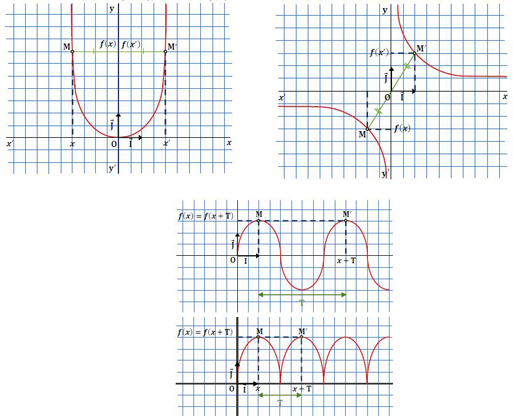
الدالة الفردية :

$f$ دالة عددية معرفة على مجال $D_{f}$ من $R$ . تكون $f$ دالة فردية اذا تحقق ما يلي :

* مهما يكن $x\in D_{f}$ فان $-x\in D_{f}$

* $f(-x) = -f(x)$

التفسير الهندسي :

اذا كانت $f$ دالة فردية فان التمثيل البياني لها يقبل المبدأ 0 كمركز تناظر .

Chargement en cours, Veuillez patientez...

ملاحظة :

- اذا كانت $f$ دالة فردية معرفة على $D_{f}$ ، فانه يمكن اقتصار دراستها على المجال $D_{f}\cap R_{+}$ فنرسم بيان الدالة $f$ على $D_{f}\cap R_{+}$ ثم نرسم الجزء الآخر بالتناظر بالنسبة للمبدأ 0 .

- $f$ دالة فردية معرفة على $D_{f}$ ، اذا كانت الدالة $f$ متزايدة على مجال من $D_{f}$ فانها متزايدة على المجال الذي يناظره من $D_{f}$ و العكس صحيح

الدالة الزوجية :

$f$ دالة عددية معرفة على مجال $D_{f}$ من $R$ . تكون $f$ دالة زوجية اذا تحقق ما يلي :

* مهما يكن $x\in D_{f}$ فان $-x\in D_{f}$

* $f(-x) = f(x)$

التفسير الهندسي :

اذا كانت $f$ دالة زوجية فان التمثيل البياني لها يقبل محور التراتيب $(yy')$ كمحور تناظر .

Chargement en cours, Veuillez patientez...

ملاحظة :

- اذا كانت $f$ دالة زوجية معرفة على $D_{f}$ ، فانه يمكن اقتصار دراستها على المجال $D_{f}\cap R_{+}$ فنرسم بيان الدالة $f$ على $D_{f}\cap R_{+}$ ثم نرسم الجزء الآخر بالتناظر بالنسبة لمحور التراتيب .

- $f$ دالة زوجية معرفة على $D_{f}$ ، اذا كانت الدالة $f$ متزايدة على مجال من $D_{f}$ فانها متناقصة على المجال الذي يناظره من $D_{f}$ و العكس صحيح

الدالة الدورية :

$f$ دالة عددية معرفة على مجال $D_{f}$ من $R$ . تكون $f$ دالة دورية اذا تحقق ما يلي :

* مهما يكن $x\in D_{f}$ فان $(x+T)\in D_{f}$ حيث $T> 0$

* $f(x+T) = f(x)$

التفسير الهندسي :

اذا كانت $f$ دالة دورية فان التمثيل البياني لها يتكرر كل مسافة $T$ من $x$ .

Chargement en cours, Veuillez patientez...

ملاحظة :

- اذا كانت $f$ دالة دورية معرفة على $D_{f}$ و دورها $T$ ، فانه يمكن اقتصار دراستها على مجال طوله $T$ ثم نكمل الرسم باستعمال انسحاب شعاعه $T.\vec{I}$

- الدوال :

* الدالة جب $sinx$ دورية ، دورها

* الدالة جب تمام $cosx$ دورية ، دورها $\pi$

* الدالة ظل $tanx$ دورية ، دورها $\pi$

* الدالة ظل تمام $cotanx$ دورية ، دورها $\pi$

الدوال المرجعية

الدوال المرجعية :

1- الدالة التآلفية : $ax+b$

2- الدالة مربع : $x^{2}$

3- الدالة مكعب : $x^{3}$

4- الدالة مقلوب : $1/x$

5- الدالة جذر التربيع : $\sqrt{x}$

6 - الدالة قيمة مطلقة : $\left | x \right |$

7 - الدالة جب : $sinx$

8 - الدالة جب تمام : $cosx$

9 - الدالة ظل : $tanx$

10 - الدالة ظل تمام : $cotanx$

الدالة التآلفية

مجال التعريف :

$D_{f}= ]-\infty ,+\infty \left [$

نوع الشفعية :

الدالة التآلفية $ax+b$ لا زوجية و لا فردية

اتجاه التغير :

اذا كان $a > 0$ فان الدالة التآلفية $ax+b$ متزايدة تماما على $R$

اذا كان $a < 0$ فان الدالة التآلفية $ax+b$ متناقصة تماما على $R$

جدول التغيرات :

Chargement en cours, Veuillez patientez...

الدالة مربع

مجال التعريف :

$D_{f}= ]-\infty ,+\infty \left [$

نوع الشفعية :

الدالة مربع $x^{2}$ دالة زوجية

اتجاه التغير :

اذا كان $x\in ] -\infty ,0 ]$ فان الدالة مربع $x^{2}$ متناقصة تماما على $R$

اذا كان $x\in \left [0,+\infty\left [$ فان الدالة مربع $x^{2}$ متزايدة تماما على $R$

جدول التغيرات :

Chargement en cours, Veuillez patientez...

الدالة مكعب

مجال التعريف :

$D_{f}= ]-\infty ,+\infty \left [$

نوع الشفعية :

االدالة مكعب $x^{3}$ دالة فردية

اتجاه التغير :

الدالة مكعب $x^{3}$ متزايدة تماما على $R$

جدول التغيرات :

Chargement en cours, Veuillez patientez...

الدالة جذر التربيع

مجال التعريف :

$D_{f}=\left [0,+\infty\left [$

نوع الشفعية :

الدالة جذر التربيع $\sqrt{x}$ لا زوجية و لا فردية

اتجاه التغير :

الدالة جذر التربيع $\sqrt{x}$ متزايدة تماما على $R$

جدول التغيرات :

Chargement en cours, Veuillez patientez...

الدالة قيمة مطلقة

مجال التعريف :

$D_{f}= ]-\infty ,+\infty \left [$

نوع الشفعية :

الدالة قيمة مطلقة $\left | x \right |$ دالة زوجية

اتجاه التغير :

اذا كان $x\in ] -\infty ,0 ]$ فان الدالة قيمة مطلقة $\left | x \right |$ متناقصة تماما على $R$

اذا كان $x\in \left [0,+\infty\left [$ فان الدالة قيمة مطلقة $\left | x \right |$ متزايدة تماما على $R$

جدول التغيرات :

Chargement en cours, Veuillez patientez...

الدالة مقلوب

مجال التعريف :

$D_{f}= ] -\infty ,0 [ \cup ] 0,+\infty [$

نوع الشفعية :

الدالة مقلوب $1/x$ دالة فردية

اتجاه التغير :

الدالة مقلوب $1/x$ متناقصة تماما على $R$

جدول التغيرات :

Chargement en cours, Veuillez patientez...

الدالة جب

الدالة جب $sinx$ :

مجال التعريف :

$D_{f}= ]-\infty ,+\infty \left [$

الشفعية و الدورية :

الدالة جب $sinx$ فردية و دورية ، دورها $\pi$

اتجاه التغير :

الدالة جب $sinx$ متزايدة تماما على $]0,\frac{\pi }{2} ]$

الدالة جب $sinx$ متناقصة تماما على $]\frac{\pi }{2},\pi]$

جدول التغيرات :

الدالة جب تمام

الدالة جب تمام $cosx$ :

مجال التعريف :

$D_{f}= ]-\infty ,+\infty \left [$

الشفعية و الدورية :

الدالة جب تمام $cosx$ زوجية و دورية ، دورها $\pi$

اتجاه التغير :

الدالة جب تمام $cosx$ متزايدة تماما على $]\frac{-\pi }{2}, 0]$

الدالة جب تمام $cosx$ متناقصة تماما على $]0,\frac{\pi }{2} ]$

جدول التغيرات :

الدالة ظل

الدالة ظل $tanx$ :

مجال التعريف :

$D_{f}= R-\left \{ \frac{\pi }{2}+K\pi \right \}$

الشفعية و الدورية :

الدالة ظل $tanx$ فردية و دورية ، دورها $\pi$

اتجاه التغير :

االدالة ظل $tanx$ متزايدة تماما على $R$

جدول التغيرات :

الدالة ظل تمام

الدالة ظل تمام $cotanx$ :

مجال التعريف :

$D_{f}= R-\left \{ K\pi \right \}$

الشفعية و الدورية :

الدالة ظل تمام $cotanx$ فردية و دورية ، دورها $\pi$

اتجاه التغير :

الدالة ظل تمام $cotanx$ متناقصة تماما على $R$

جدول التغيرات :

العمليات الجبرية

$f$ و $g$ دالتان معرفتان على $D_{f}$ و $D_{g}$ على الترتيب و $\lambda$ عدد حقيقي .

الجدول : أنظر الشكل المقابل

تركيب الدوال

تركيب الدوال :

$f$ و $g$ دالتان معرفتان على $D_{f}$ و $D_{g}$ على الترتيب بحيث من أجل كل $x$ من $D_{f}$ فان : $f(x)\in D_{g}$

مركب الدالة $f$ متبوعة بالدالة $g$ هي الدالة التي نرمز لها بـ $fog$ و المعرفة على $D_{f}$ بـ : $(fog)(x)=f\left [ g(x) \right ]$

مجموعة تعريف دالة مركبة :

$f$ و $g$ دالتان معرفتان على $D_{f}$ و $D_{g}$ على الترتيب ، مجموعة تعريف الدالة $gof$ هو المجال $D_{gof}$ حيث :

* $x\in D_{g}$ ( لأن السابقة $x$ هي المتغير في الدالة $g$ )

* $g(x)\in D_{f}$ ( لأن الصورة $g(x)$ هي المتغير في الدالة $f$ )

- عملية تركيب الدوال هو عملية تجميعية أي أن : $(fog)oh = fo(goh)$

- عملية تركيب الدوال ليس عملية تبديلية أي أن : $fog \neq gof$

اتجاه تغير مجموع دالتين :

* مجموع دالتين متزايدتين (أو متزايدتين تماما) على مجال $I$ هو دالة متزايدة (أو متزايدة تماما) على $I$

* مجموع دالتين متناقصتين (أو متناقصتين تماما) على مجال $I$ هو دالة متناقصة (أو متناقصة تماما) على $I$

اتجاه تغير جداء دالتين :

* جداء دالتين متزايدتين (أو متزايدتين تماما) على مجال $I$ هو دالة متزايدة (أو متزايدة تماما) على $I$

* جداء دالتين متناقصتين (أو متناقصتين تماما) على مجال $I$ هو دالة متناقصة (أو متناقصة تماما) على $I$

تنبيه! لا يمكن استنتاجه :

لا يمكن استنتاج اتجاه تغير مجموع أو جداء دالتين مختلفتين في اتجاه التغير لأنه لا يمكن جمع أو ضرب متبانيتين مختلفتين في الاتجاه .

اتجاه تغير مجموع دالة و عدد :

$f$ دالة معرفة على مجال $E$ من $R$ و $k$ عدد حقيقي .

* للدالة $f$ و الدالة $f\pm k$ نفس اتجاه التغير

اتجاه تغير جداء دالة و عدد :

$f$ دالة معرفة على مجال $E$ من $R$ و $k$ عدد حقيقي .

* اذا كان $k> 0$ فان للدالة $f$ و الدالة $f\times k$ لهما نفس اتجاه التغير

* اذا كان $k< 0$ فان للدالة $f$ و الدالة $f\times k$ مختلفتان في اتجاه التغير

اتجاه تغير مركب دالتين :

$f$ و $g$ دالتان معرفتان على $D_{f}$ و $D_{g}$ على الترتيب بحيث من أجل كل $x$ من $D_{f}$ فان : $f(x)\in D_{g}$

* اذا كانت للدالتين $f$ و $g$ نفس اتجاه التغير فان الدالة $fog$ تكون متزايدة .

* اذا كانت للدالتين $f$ و $g$ اتجاه التغير مختلف فان الدالة $fog$ تكون متناقصة .