ملخص الدرس / الثآنية ثانوي/رياضيات/الإحصاء و الإحتمالات/الإحصاء
الربعيات
 تعريف :
تعريف :
* الربعي الأول لسلسلة إحصائية هو اصغر قيمة للطبع الإحصائي حيث يكون
على الأقل من الحدود لها قيمة أصغر أو يساوي
.
* الربعي الثالث لسلسلة إحصائية هو اصغر قيمة للطبع الإحصائي حيث يكون
على الأقل من الحدود لها قيمة أصغر أو يساوي
.
ملاحظة :
و
قيمتان من السلسلة بخلاف الوسيط
الذي يمكن أن لا يكون قيمة من السلسلة .
 كيف نحدد
كيف نحدد 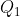 و
و 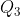 :
:
* بعد ترتيب القائمة ترتيبا تصاعديا ( مع كتابة كل قيمة بعدد مساو لتكرارها )
* القيمة التي رتبتها
حيث
هو أصغر عدد طبيعي يحقق
.
* القيمة التي رتبتها
حيث
هو أصغر عدد طبيعي يحقق
.
في حالة طبع كمي متقطع :
نطبق التعريف باستخدام التكرار المجمع الصاعد أو التواتر المجمع الصاعد.
في حالة طبع كمي مستمر :
* هي فاصلة النقطة من منحنى التواتر المجمع الصاعد التي ترتيبها
.
* هي فاصلة النقطة من منحنى التواتر المجمع الصاعد التي ترتيبها
.
العشريان d1وd2
تعريف :
* العشري الأول لسلسلة إحصائية هو أصغر قيمة طبع حيث يكون
على الاقل من الحدود لها قيمة طبع أصغر أو تساوي
.
* العشري الأول لسلسلة إحصائية هو أصغر قيمة طبع حيث يكون
على الاقل من الحدود لها قيمة طبع أصغر أو تساوي
.
خواص الربعيات
 الإنحراف الربعي :
الإنحراف الربعي :
تعريف :
الإنحراف الربعي هو الفرق بين الربعيين الثالث و الأول . أي هو العدد حيث
ملاحظة 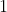 :
:
الانحراف الربعي هو مؤشر من مؤشرات التشتت .
ملاحظة 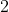 :
:
في مضلع سلسلة مستمرة المستقيمات التي معادلاتها ،
،
تقسم المضلع إلى أربعة مجالات متساوية المساحات .
 المخطط بالعلب :
المخطط بالعلب :
نكون مخططا بالعلب بالطريقة التالية :
* نضع قيم الطبع على محور ( أفقي أو شاقولي )
* نعين على هذا المحور القيم ،
،
،
و
. ( القيمة الصغرى ، القيمة الكبرى ، الربعيين الأول و الثالث و الوسيط )
* نكون عندئذ مستطيلا ( العلبة ) بالتوازي مع المحور . ( طول المستطيل هو الانحراف الربعي و عرضه كيفي )
مثال : ،
،
،
و
.
ملاحظة :
هذا المخطط يمكننا من مشاهدة تشتت توزيع إحصائي و المقارنة بين عدة سلاسل إحصائية .
 أثر تغيير تآلفي على الربعيين :
أثر تغيير تآلفي على الربعيين :
مبرهنة  :
:
سلسلة إحصائية
وسيطها
و ربيعييها الأول و الثالث هما
و
السلسلة الاحصائية
بنفس التكرارات حيث من اجل كل
لدينا
نرمز لوسيطها ب
و اربعييها الأول و الثالث ب
و
على الترتيب عندئذ
و من أجل
لدينا :
و
.
التباين و الانحراف المعياري
تعريف :
نعتبر السلسلة حيث
هي قيم الطبع و
تكراراتها مع
نسمي تباين السلسلة الاحصائية العدد الحقيقي الذس نرمز له بالرمز
و المعرف بالعلاقة :
مع و
الوسط الحسابي للسلسلة .
* إذا كانت هي تواترات السلسلة حيث
فإن :
يسمى العدد الحقيقي الانحراف المعياري و يرمز له بالرمز
ة نكتب
.
مع و
عدد حقيقي موجب .
ملاحظة :
إذا كانت السلسلة مجمعة بالفئات ( توزيع منتظم ) نأخذ كمركز للفئة .
مبرهنة :
نعتبر السلسلة حيث
هي قيم الطبع و
تكراراتها مع
و
عدد طبيعي أكبر تماما من
.يمكن كتابة
على الشكل :
تستعمل هذه العبارة عادة لحساب دون حساب
ملاحظة  :
:
إذا كانت قيم الطبع ذات وحدات معبنة ( أطوال ، زمن ، ...) فإن
يحسب بهذه الوحدات مربعة ( مساحة ، زمن مربع ، ...) و بالتالي فإن وحدة
هي وحدة
.
ملاحظة  :
:
يستعمل أحيانا مؤشر تشتت آخر يسمى الوسط الحسابي للانحرافات المطلقة و هو العدد الحقيقي حيث
مع
هي قيم الطبع ،
الوسط الحسابي ،
التواترات و
خواص التباين و الانحراف المعياري
) الخاصية الأساسية :
الخاصية الأساسية :
مبرهنة :
الدالة المعرفة كما يلي
تقبل قيمة حدية صغرى عندما
هذه القيمة هي التباين
مع
قيم الطبع ،
تكراراتها ،
) التغيير التآلفي :
التغيير التآلفي :
مبرهنة :
إذا كانت سلسلة احصائية تباينها
و انحرافها المعياري
و
سلسلة احصائية بنفس التكرار
و انحرافها المعياري
و
مع من أجل
يكون لدينا
و
تلخيص سلسلة احصائية
* يتم تلخيص سلسلة إحصائية بمؤشرين ( مؤشر موقع و مؤشر تشتت )
* عموما نختار الثنائية ( الوسيط ، الوسط الحسابي للانحرافات المطلقة ) ( ،
)أو الثنائية ( الوسط الحسابي ، الانحراف المعياري ) اي (
،
)
*يمكن استعمال ثنائيات أخرى لتلخيص سلسلة كالثنائية ( الوسيط ، المدى ) يكن يعاب على المدى تأثره بالقيم الشاذة .
*تستخدم احيانا الثنائية ( الوسيط ، الانحراف الربعي ) لتلخيص السلسلة و هي ثنائية لا تتأثر بالقيم الشاذة .
* تلخيص سلسلة إحصائية يمكّننا من مقارنتها بسلسلة أخرى ملخصة باستعمال الثنائية المختارة .