ملخص الدرس / الثآنية ثانوي/رياضيات/الهندسة/الهندسة في الفضاء

الدرس

التعليم في الفضاء

$.1$ المعلم الديكارتي :

تعريف :

نسمي معلما للفضاء مبدؤه النقطة $O$ كل رباعية نقط $\left ( O;I,J,K \right )$ ليست من نفس المستوي .

إذا وضعنا : $\overrightarrow{OI}=\vec{i}$ ، $\overrightarrow{OJ}=\vec{j}$ و $\overrightarrow{OK}=\vec{k}$ نرمز إلى المعلم السابق بالرمز $\left ( O;\vec{i},\vec{j},\vec{k} \right )$ .

ملاحظات :

* تشكل النقط $O$ ، $I$ ، $J$ و $K$ رباعي وجوه .

* الاشعة $\vec{i}$ ، $\vec{j}$ و $\vec{k}$ ليست من نفس المستوي .

* يسمى المستقيم $\left ( OI \right )$ محور الفواصل و المستقيم $\left ( OJ \right )$ محور التراتيب بينما يسمى المستقيم $\left ( OK \right )$ محور الرواقم .

*إذا كانت المستقيمات $\left ( OI \right )$ ، $\left ( OJ \right )$ و $\left ( OK \right )$ متعامدة مثنى مثنى نقول أن المعلم $\left ( O;I,J,K \right )$ متعامد .

* إذا كان $\left ( O;I,J,K \right )$ معلما متعامدا و كان $OI=OJ=OK=1$ نقول أن $\left ( O;I,J,K \right )$ متعامد و متجانس .

* نرمز إلى المستوي $\left ( OIJ \right )$ ب $P\left ( O;\vec{i},\vec{j} \right )$ و إلى إلى المستوي $\left ( OJK \right )$ ب $P\left ( O;\vec{j},\vec{k} \right )$ ، ...

$.2$ إحداثيات نقطة :

مبرهنة :

إذا كان $\left ( O;\vec{i},\vec{j},\vec{k} \right )$ معلما للفضاء و كانت $M$ نقطة من الفضاء فإنه توجد ثلاثية أعداد حقيقية وحيدة $\left ( x,y,z \right )$ بحيث : $\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}$

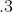$.3$ إحداثيات شعاع :

تعريف :

$\left ( O;\vec{i},\vec{j},\vec{k} \right )$ معلم للفضاء . $\vec{u}$ شعاع و لتكن $M$ النقطة الوحيدة التي تحقق $\overrightarrow{OM}=\vec{u}$ .

إحداثيات الشعاع $\vec{u}$ هي $\left ( x,y,z \right )$ إحداثيات النقطة $M$ في المعلم $\left ( O;\vec{i},\vec{j},\vec{k} \right )$ . و يمكن أن نكتب $\overrightarrow{OM}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$

و هكذا كل شعاع $\vec{u}$ يكتب بطريقة وحيدة على الشكل : $\vec{u}=x\vec{i}+y\vec{j}+z\vec{k}$

الحساب على الاحداثيات

$.1$ خواص الاحداثيات :

يتم تمديد كل النتائج الخاصة بالاحداثيات في المستوي إلى الفضاء .

نتائج :

$\left ( O;\vec{i},\vec{j},\vec{k} \right )$ معلم للفضاء .

$(1$ إذا كان $\vec{u}\left ( x,y,z \right )$ و $\vec{v}\left ( {x}',{x}',{z}' \right )$ شعاعين من الفضاء و كان $\alpha$ عددا حقيقيا فإن :

* $\vec{u}=\vec{0}$ يعني $x=y=z=0$ .

* $\vec{u}=\vec{v}$ يعني $x={x}'$ و $y={y}'$ و $z={z}'$ .

* إحداثيات $\left ( \vec{u}+\vec{v} \right )$ هي $\left ( x+{x}',y+{y}',z+{z}' \right )$ و احداثيات $\alpha \vec{u}$ هي $\left ( \alpha x,\alpha y,\alpha z \right )$ .

$(2$ إذا كانت $A\left ( x_{A},y_{A},z_{A} \right )$ و $B\left ( x_{B},y_{B},z_{B} \right )$ نقطتين من الفضاء فإن :

* إحداثيات الشعاع $\overrightarrow{AB}$ هي $\left ( x_{B}-x_{A},y_{B}-y_{A},z_{B}-z_{A} \right )$ .

* إحداثيات منتصف القطعة المستقيمة $\left [ AB \right ]$ هي $\left ( \frac{x_{A}+x_{B}}{2},\frac{y_{A}+y_{B}}{2},\frac{z_{A}+z_{B} }{2}\right )$ .

$.2$ الأشعة من نفس المستوي :

$\left ( O;\vec{i},\vec{j},\vec{k} \right )$ معلم للفضاء . $\vec{u}\left ( a,b,c \right )$ ، $\vec{v}\left ( {a}',{b}',{c}' \right )$ و $\vec{w}\left ( {a}'',{b}'',{c}'' \right )$ ثلاثة أشعة من الفضاء .

تكون الأشعة $\vec{u}$ ، $\vec{v}$ و $\vec{w}$ من نفس المستوي إذا و فقط إذا وجد عددان حقيقيان $x$ و $y$ بحيث $\vec{w}=x\vec{u}+y\vec{v}$ .

و هذا يعني أن الجملة $\left\{\begin{matrix} ax+{y}'={a}''\\ bx+{b}'y={b}''\\ cx+{c}'y={c}'' \end{matrix}\right.$ تقبل حلا $\left ( x,y \right )$ في $\mathbb{R}^{2}$ .

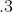$.3$ معادلات مستقيم معرف بنقطة و شعاع توجيه له :

$\left ( O;\vec{i},\vec{j},\vec{k} \right )$ معلم للفضاء . ليكن $\left ( D \right )$ المستقيم الذي يشمل النقطة $A\left ( x_{A},y_{A},z_{A} \right )$ و $\vec{u}\left ( a,b,c \right )$ شعاع توجيه له .

$M\left ( x,y,z \right )\in \left ( D \right )$ يعني $\overrightarrow{AM}=\alpha \vec{u}$ $\left ( \alpha \in \mathbb{R} \right )$ أي $x-x_{A}=\alpha a$ و $y-y_{A}=\alpha b$ و $z-z_{A}=\alpha c$ .

و هذا يعني إذا كان $abc \neq 0$ أن $\frac{x-x_{A}}{a}=\frac{y-y_{A}}{b}=\frac{z-z_{A}}{c}$ اي أن مثلا : $\left\{\begin{matrix} b\left ( x-x_{A}-a\left ( y-y_{A} \right )=0 \right )\\ c\left ( x-x_{A}-a\left ( y-y_{A} \right )=0 \end{matrix}\right.$

أما إذا كان أحد الأعداد $a$ ، $b$ أو $c$ معدوما فإن مثلا في حالة $c=0$ : $\left\{\begin{matrix} b\left ( x-x_{A}-a\left ( y-y_{A} \right )=0 \\ z=z_{A} \end{matrix}\right.$

أما إذا انعدم عددان من الأعداد $a$ ، $b$ و $c$ فإن مثلا في حالة $a=b=0$ : $\left\{\begin{matrix} x=x_{A}\\ y=y_{A} \end{matrix}\right.$ و يبقى $z$ كيفي .

حالات خاصة :

نرمز إلى محور الفواصل ب $\left ( Ox \right )$ ، إلى محور التراتيب ب $\left ( Oy \right )$ و إلى محور الرواقم ب $\left ( Oz \right )$ الجدول التالي يحدد الشروط الكافية و اللازمة التي يجب أن تحققها $\left ( x,y,z \right )$ إحداثيات

نقطة $M$ لكي تنتمي إلى المحور المعني :

المحور	$\left ( Ox \right )$	$\left ( Oy \right )$	$\left ( Oz \right )$
مميزاته	$y=z=0$	$z=x=0$	$x=y=0$

المسافة بين نقطتين

$.1$ العبارة التحليلية لطويلة شعاع :

مبرهنة :

في معلم متعامد و متجانس تحسب طويلة الشعاع $\vec{u}\left ( x,y,z \right )$ ب : $\left \| \vec{u} \right \|=\sqrt{x^{2}+y^{2}+z^{2}}$ .

$.2$ المسافة بين نقطتين :

مبرهنة :

في معلم متعامد و متجانس تحسب المسافة بين نقطتين $A\left ( x_{A},y_{A},z_{A} \right )$ و $B\left ( x_{B},y_{B},z_{B} \right )$ ب :

$AB=\sqrt{\left ( x_{B}-x_{A} \right )^{2}+\left ( y_{B}-y_{A} \right )^{2}+\left ( z_{B}-z_{A} \right )^{2}}$

ملاحظة :

عند إجراء الحسابات غاليا ما يفضل مربع المسافة على المسافة .

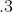$.3$ معادلة سطح كرة مركزها مبدأ المعلم :

$\left ( O;\vec{i},\vec{j},\vec{k} \right )$ معلم متعامد و متجانس للفضاء . $\alpha$ عدد حقيقي موجب تماما . $\left ( S \right )$ سطح الكرة التي مركزها $O$ و نصف قطرها $\alpha$ . لتكن $M\left ( x,y,z \right )$

نقطة كيفية من الفضاء .

$M\in \left ( S \right )$ يعني $OM=\alpha$ أي $OM^{2}=\alpha ^{2}$ و هذا يعني $x^{2}+y^{2}+z^{2}=\alpha ^{2}$

إذن $x^{2}+y^{2}+z^{2}=\alpha ^{2}$ هي معادلة سطح الكرة $\left ( S \right )$ التي مركزها $O$ و نصف قطرها $\alpha$ .