ملخص الدرس / الثآنية ثانوي/رياضيات/الهندسة/الزوايا الموجهة و حساب المثلتات

الدرس

من الأستاذ(ة) وزارة التربية الوطنية

الزوايا الموجهة

$.1$ زاوية موجهة لشعاعين غير معدومين :

يوجه المستوي توجيها مباشرا ( أو توجيها موجبا ) و يسمى الاتجاه الآخر الاتجاه غير المباشر ( أو الاتجاه السالب ) .

اصطلاحا نختار الاتجاه المباشر الاتجاه المعاكس لدوران عقارب الساعة .

في المستوي الموجه نسمي دائرة مثلثية كل دائرة موجهة في الاتجاه المباشر و التي نصف قطرها $1$ .

في كل ما يأتي نعتبر المستوي الموجه :

تعريف :

ليكن $\vec{u}$ و $\vec{v}$ شعاعين غير معدومين .

الثنائية $\left ( \vec{u},\vec{v} \right )$ تسمى زاوية موجهة لشعاعين .

Chargement en cours, Veuillez patientez...

$.2$ قيس زاوية موجهة :

تعريف :

ليكن $\vec{u}$ و $\vec{v}$ شعاعين غير معدومين .

إذا كان $x$ قيسا للزاوية الموجهة $\left ( \vec{u},\vec{v} \right )$ فإن كل الأعداد من الشكل $x+2k\pi$ هي أقياس للزاوية $\left ( \vec{u},\vec{v} \right )$ . مع $k\in \mathbb{Z}$ .

خاصية :

من بين أقياس الزاوية الموجهة $\left ( \vec{u},\vec{v} \right )$ يوجد قيس وحيد على المجال $\left ¨]-\pi ,\pi \right ]$ يسمى القيس الرئيسي للزاوية الموجهة $\left ( \vec{u},\vec{v} \right )$ .

نتائج :

$(1$ القيس الرئيسي للزاوية المعدومة $\left ( \vec{u},\vec{u} \right )$ هو $0$ .

$(2$ القيس الرئيسي للزاوية المستقيمة $\left ( \vec{u},-\vec{u} \right )$ هو $\pi$ .

$(3$ القيس الرئيسي للزاوية القائمة المباشرة هو $\frac{\pi }{2}$ .

$(4$ القيس الرئيسي للزاوية القائمة غير المباشرة هو $-\frac{\pi }{2}$ .

$(5$ إذا كان $x$ القيس الرئيسي للزاوية الموجهة $\left ( \vec{u},\vec{v} \right )$ فإن $\left | x \right |$ هو قيس للزاوية الهندسية المكونة من $\vec{u}$ و $\vec{v}$ .

$.2$ علاقة شال :

مبرهنة : (تقبل بدون برهان )

من أجل كل ثلاثة أشعة غير معدومة $\vec{u}$ ، $\vec{v}$ و $\vec{w}$ لدينا : $\left ( \vec{u},\vec{v} \right )+\left ( \vec{v},\vec{w} \right )=\left ( \vec{u},\vec{w} \right )$ .

نتائج :

من أجل كل شعاعين غير معدومين $\vec{u}$ و $\vec{v}$ لدينا :

* $\left ( \vec{v},\vec{u} \right )=-\left ( \vec{u},\vec{v} \right )$ .

* $\left ( \vec{u},\vec{-v} \right )=\left ( \vec{u},\vec{v} \right )+\pi$ .

* $\left ( -\vec{u},\vec{v} \right )=\left ( \vec{u},\vec{v} \right )+\pi$ .

* $\left ( -\vec{u},-\vec{v} \right )=\left ( \vec{u},\vec{v} \right )$ .

خواص الزوايا الموجهة

$.1$ الزوايا الموجهة المتقايسة :

خاصية :

$\vec{u}$ ، $\vec{v}$ ، $\vec{{u}'}$ و $\vec{{v}'}$ أشعة غير معدومة من المستوي ، ليكن $\alpha$ قيسا للزاوية $\left ( \vec{u},\vec{v} \right )$ و ${\alpha}'$ قيسا للزاوية $\left ( \vec{{u}'},\vec{{v}'} \right )$

تكون الزاويتان $\left ( \vec{u},\vec{v} \right )$ و $\left ( \vec{{u}'},\vec{{v}'} \right )$ متقايستين إذا و فقط إذا وجد عددى صحيح $k$ حيث ${\alpha }'=\alpha +2k\pi$ .

ملاحظة :

وجود عدد صحيح $k$ حيث ${\alpha }'=\alpha +2k\pi$ معناه ${\alpha }'-\alpha$ مضاعف ل $2\pi$ .

إذا كان ${\alpha }'=\alpha +2k\pi$ نقول أن $\alpha$ و ${\alpha }'$ قيسان لنفس الزاوية أو قيسان ازاويتان متقايستين .

$.2$ الزوايا الموجهة و الارتباط الخطي لشعاعين :

خاصية :

$\vec{u}$ و $\vec{v}$ شعاعان غير غير معدومين من المستوي .

يكون الشعاعان $\vec{u}$ و $\vec{v}$ مرتبطان خطيا إذا و فقط إذا كان : $\left ( \vec{u},\vec{v} \right )=2k\pi$ أو $\left ( \vec{u},\vec{v} \right )=\pi +2k\pi$ . $k\in \mathbb{Z}$

ملاحظة :

* إذا كان $\left ( \vec{u},\vec{v} \right )=2k\pi$ يكون للشعاعين $\vec{u}$ و $\vec{v}$ نفس الاتجاه .

*إذا كان $\left ( \vec{u},\vec{v} \right )=\pi +2k\pi$ يكون للشعاعين $\vec{u}$ و $\vec{v}$ اتجاهين متعاكسين .

خاصية :

$\vec{u}$ و $\vec{v}$ شعاعان غير غير معدومين من المستوي . ليكن $k$ و ${k}'$ عددين حقيقيين غير معدومين .

* إذا كان $k$ و ${k}'$ من نفس الاشارة فإن $\left (k \vec{u},{k}'\vec{v} \right )=\left ( \vec{u},\vec{v} \right )$ .

* إذا كان $k$ و ${k}'$ من اشارتين مختلفتين فإن $\left (k \vec{u},{k}'\vec{v} \right )=\left ( \vec{u},\vec{v} \right )+\pi$ .

$.3$ الزاوية المحيطية :

$\left ( C \right )$ دائرة مثلثية مركزها $O$ . $A$ ، $B$ و $M$ ثلاث نقط متمايزة مثنى مثنى من الدائرة $\left ( C \right )$ . الزاوية الموجهة $\left ( \overrightarrow{MA},\overrightarrow{MB} \right )$ تسمى زاوية محيطية .

مبرهنة :

إذا كانت $A$ ، $B$ و $M$ ثلاث نقط متمايزة مثنى مثنى من دائرة مثلثية $\left ( C \right )$ مركزها $O$ . و إذا كان $\alpha$ قيسا للزاوية الموجهة $\left ( \overrightarrow{OA},\overrightarrow{OB} \right )$ . فإن $\frac{\alpha }{2}$ قيس للزاوية $\left ( \overrightarrow{MA},\overrightarrow{MB} \right )$ .

Chargement en cours, Veuillez patientez...

حساب المثلثات

تعريف :

إذا كان $\left ( \vec{i},\vec{j} \right )=\frac{\pi }{2}$ نقول أن المعلم المتعامد و التجانس $\left ( O;\vec{i};\vec{j} \right )$ من المستوى مباشر .

إذا كان $\left ( \vec{i},\vec{j} \right )=-\frac{\pi }{2}$ نقول أن المعلم المتعامد و التجانس $\left ( O;\vec{i};\vec{j} \right )$ من المستوى غير مباشر .

* معلم متعامد و متجانس مباشر . Chargement en cours, Veuillez patientez...

* معلم متعامد و متجانس غير مباشر . Chargement en cours, Veuillez patientez...

$.2$ جيب تمام و جيب زاوية موجهة لشعاعين :

تذكير و تعريف :

$\left ( C \right )$ دائرة مثلثية مركزها $O$ . لتكن $A$ و $B$ نقطتين من الدائرة $\left ( C \right )$ حيث أن $\left ( O,\overrightarrow{OA},\overrightarrow{OB} \right )$ معلم متعامد و متجانس مباشر .

نضع $\overrightarrow{OA}=\vec{i}$ و $\overrightarrow{OB}=\vec{j}$ ، لكل عدد حقيقي $x$ صورة $M$ على الدائرة $\left ( C \right )$ حيث $x$ قيس بالراديان للزاوية الموجهة $\left ( \vec{i},\overrightarrow{OM} \right )$ ، نعلم أن جيب تمام العدد $x$

هو فاصلة النقطة $M$ و نكتب $\cos x$ و أن جيب العدد $x$ هو ترتيب النقطة $M$ و نكتب $\sin x$ .

إذا كان $x$ قيسا بالراديان للزاوية الموجهة $\left ( \vec{i},\overrightarrow{OM} \right )$ فإن كل عدد من الشكل $x+2k\pi$ حيث $k$ عدد صحيح هو كذلك قيس بالراديان للزاوية الموجهة $\left ( \vec{i},\overrightarrow{OM} \right )$ ومنه :

$x$ و $x+2k\pi$ لهما نفس الصورة $M$ على الدائرة $\left ( C \right )$ . و بالتالي :

$\cos \left ( x+2k\pi \right )=\cos x$ و $\sin \left ( x+2k\pi \right )=\sin x$ مع $k\in \mathbb{Z}$

نقول أن الدالتين دوريتان و $2\pi$ دور لهما .

Chargement en cours, Veuillez patientez...

نتائج :

من أجل كل عدد حقيقي $x$ :

$-1\leq \cos x\leq 1$ ، $-1\leq \sin x\leq 1$ ، $\cos ^{2}x+\sin ^{2}x=1$ .

جدول القيم الشهيرة :

$\frac{\pi }{2}$	$\frac{\pi }{3}$	$\frac{\pi }{4}$	$\frac{\pi }{6}$	$0$	$x$
$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$	$\sin x$
$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$	$\cos x$

تعريف :

* جيب تمام زاوية موجهة $\left ( \vec{u},\vec{v} \right )$ هو جيب تمام أحد أقياسها بالراديان و نرمز له بالرمز $\cos \left ( \vec{u},\vec{v} \right )$ .

* جيب زاوية موجهة $\left ( \vec{u},\vec{v} \right )$ هو جيب أحد أقياسها بالراديان و نرمز له بالرمز $\sin \left ( \vec{u},\vec{v} \right )$ .

جيب تمام و جيب الزوايا المرفقة

تعريف :

نسمي الزوايا المرفقة بزاوية موجهة حيث $x$ قيس لها ، الزوايا الموجهة التي أحد أقياسها : $-x$ ، $\pi -x$ ، $\pi +x$ ، $\frac{\pi }{2}-x$ ، $\frac{\pi }{2}+x$ .

فيما يلي نأخذ 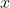$x$ عددا حقيقيا و 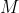$M$ صورته على دائرة مثلثية المرفقة بالمعلم المتعامد و المتجانس $\left ( O;\vec{i};\vec{j} \right )$ .

مبرهنة $1$ :

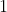من أجل كل عدد حقيقي $x$ لدينا :

$\left ( 1 \right ) \left\{\begin{matrix} \cos \left ( \pi +x \right )=-\cos x\\ \sin \left ( \pi +x \right )=-\sin x \end{matrix}\right.$ ، $\left (2 \right ) \left\{\begin{matrix} \cos \left ( \pi -x \right )=-\cos x\\ \sin \left ( \pi -x \right )=\sin x \end{matrix}\right.$ ، $\left ( 3 \right ) \left\{\begin{matrix} \cos \left ( -x \right )=\cos x\\ \sin \left ( -x \right )=-\sin x \end{matrix}\right.$

* الجملة $\left ( 1 \right )$ : $M$ و ${M}'$ متناظرتان بالنسبة إلى مبدأ المعلم . Chargement en cours, Veuillez patientez...

* الجملة $\left ( 2 \right )$ : $M$ و ${M}'$ متناظرتان بالنسبة إلى محور التراتيب . Chargement en cours, Veuillez patientez...

* الجملة $\left ( 3 \right )$ : $M$ و ${M}'$ متناظرتان بالنسبة إلى مبدأ الفواصل . Chargement en cours, Veuillez patientez...

ملاحظة :

من الجملة $\left ( 3 \right )$ نستنتج أن الدالة $\cos$ ( جيب تمام ) دالة زوجية و أن الدالة $\sin$ ( جيب ) دالة فردية .

مبرهنة $2$ :

من أجل كل عدد حقيقي $x$ لدينا :

$\left\{\begin{matrix} \cos \left ( \frac{\pi }{2}+x \right )=-\sin x\\ \sin \left ( \frac{\pi }{2}+x \right )=\cos x \end{matrix}\right.$

$\left\{\begin{matrix} \cos \left ( \frac{\pi }{2}-x \right )=\sin x\\ \sin \left ( \frac{\pi }{2}-x \right )=\cos x \end{matrix}\right.$

معادلات مثلثية

$.1$ عددين حقيقيين لهما نفس الجيب تمام و نفس الجيب :

ليكن $a$ و $b$ عددين حقيقيين .

* $\cos a=\cos b$ معناه $a=b+2k\pi$ أو $a=-b+2k\pi$ مع $k\in \mathbb{Z}$ .

* $\sin a=\sin b$ معناه $a=b+2k\pi$ أو $a=\pi -b+2k\pi$ مع $k\in \mathbb{Z}$ .

$.2$ المعادلات المثلثية الأساسية :

أ- المعادلات من الشكل $\cos x=a$ حيث $a$ عدد حقيقي :

إذا كان $a<-1$ أو $a>1$ االمعادلة لا تقبل حلولا .

إذا كان $-1\leq a\leq 1$ يوجد عدد حقيقي $c$ حيث $a=\cos c$ و الحلول هي : [ $x=c+2k\pi$ أو $x=-c+2k\pi$ ] .

ب- المعادلات من الشكل $\sin x=a$ حيث $a$ عدد حقيقي :

إذا كان $a<-1$ أو $a>1$ االمعادلة لا تقبل حلولا .

إذا كان $-1\leq a\leq 1$ يوجد عدد حقيقي $c$ حيث $a=\sin c$ و الحلول هي : [ $x=c+2k\pi$ أو $x=\pi -c+2k\pi$ ] .

الاحداثيات القطبية

$.1$ التعليم القطبي :

ليكن $\left ( O;\vec{i};\vec{j} \right )$ معلم مباشر متعامد و متجانس . لتكن $\left ( C \right )$ الدائرة المثلثية التي مركزها $O$ .

تعريف :

من أجل كل نقطة $M$ غير منطبقة على $O$ ، الثنائية $\left ( r,\theta \right )$ ، حيث $OM=r$ و $\theta =\left ( \vec{i},\overrightarrow{OM} \right )$ ، تسمى ثنائية إحداثيات قطبية في المستوي للنقطة $M$ و نرمز $M\left ( r,\theta \right )$

( $r$ عدد حقيقي موجب تماما و $\theta$ عدد حقيقي ) .

النقطة $O$ تسمى القطب ، $\left ( O;\vec{i}\right )$ يسمى المحور القطبي ، نقول أن $r$ هو نصف القطر القطبي و $\theta$ إحدى الزوايا القطبية .

في الشكل $OM=2\sqrt{2}$ و $\left ( \vec{i},\overrightarrow{OM} \right )=\frac{3\pi }{4}$ إذا الاحداثيات القطبية للنقطة $M$ هي : $\left ( 2\sqrt{2};\frac{3\pi }{4} \right )$ .

في الشكل $O{M}'=\sqrt{5}$ و $\left ( \vec{i},\overrightarrow{OM} \right )=\frac{5\pi }{6}$ إذا الاحداثيات القطبية للنقطة $M$ هي : $\left ( \sqrt{5};\frac{5\pi }{6} \right )$ .

Chargement en cours, Veuillez patientez...

ملاحظة :

الثنائية $M\left ( r,\theta \right )$ تعرف نقطة وحيدة $M$ .

$.2$ العلاقة بين الاحداثيات القطبية و الاحداثيات الديكارتية :

مبرهنة :

في معلم مباشر متعامد و متجانس $\left ( O;\vec{i};\vec{j} \right )$ لتكن $\left ( C \right )$ الدائرة المثلثية . إذا كانت $M$ غير منطبقة على $O$ و كانت احداثياها الديكارتية $\left ( x,y \right )$ و احداثياها القطبية $\left ( r,\theta \right )$ فإن :

$y=r\sin \theta \: \: ;\: \: x=r\cos \theta \: \: ;\: r=\sqrt{x^{2}+y^{2}}$ .

ملخص الدرس / الثآنية ثانوي/رياضيات/الهندسة/الزوايا الموجهة و حساب المثلتات

الدرس

الزوايا الموجهة

زاوية موجهة لشعاعين غير معدومين :

في كل ما يأتي نعتبر المستوي الموجه :

تعريف :

قيس زاوية موجهة :

تعريف :

خاصية :

نتائج :

علاقة شال :

مبرهنة : (تقبل بدون برهان )

نتائج :

خواص الزوايا الموجهة

الزوايا الموجهة المتقايسة :

خاصية :

ملاحظة :

الزوايا الموجهة و الارتباط الخطي لشعاعين :

خاصية :

ملاحظة :

خاصية :

الزاوية المحيطية :

مبرهنة :

حساب المثلثات

تعريف :

جيب تمام و جيب زاوية موجهة لشعاعين :

تذكير و تعريف :

نتائج :

جدول القيم الشهيرة :

تعريف :

جيب تمام و جيب الزوايا المرفقة

تعريف :

فيما يلي نأخذ عددا حقيقيا و صورته على دائرة مثلثية المرفقة بالمعلم المتعامد و المتجانس .

مبرهنة :

ملاحظة :

مبرهنة :

معادلات مثلثية

عددين حقيقيين لهما نفس الجيب تمام و نفس الجيب :

المعادلات المثلثية الأساسية :

الاحداثيات القطبية

التعليم القطبي :

تعريف :

ملاحظة :

العلاقة بين الاحداثيات القطبية و الاحداثيات الديكارتية :

مبرهنة :

$.1$ زاوية موجهة لشعاعين غير معدومين :

$.2$ قيس زاوية موجهة :

$.2$ علاقة شال :

$.1$ الزوايا الموجهة المتقايسة :

$.2$ الزوايا الموجهة و الارتباط الخطي لشعاعين :

$.3$ الزاوية المحيطية :

$.2$ جيب تمام و جيب زاوية موجهة لشعاعين :

فيما يلي نأخذ $x$ عددا حقيقيا و $M$ صورته على دائرة مثلثية المرفقة بالمعلم المتعامد و المتجانس $\left ( O;\vec{i};\vec{j} \right )$ .

مبرهنة $1$ :

مبرهنة $2$ :

$.1$ عددين حقيقيين لهما نفس الجيب تمام و نفس الجيب :

$.2$ المعادلات المثلثية الأساسية :

$.1$ التعليم القطبي :

$.2$ العلاقة بين الاحداثيات القطبية و الاحداثيات الديكارتية :