ملخص الدرس / الرابعة متوسط/رياضيات/الدوال و تنظيم المعطيات/الاحصاء
الملخص
من الأستاذ(ة) ELBEY Mouloudالتوزيعات التكرارية
1) التوزيعات التكرارية:
- تكرار قيمة لميزة إحصائية هو عدد الأفراد الموافقة لهذه القيمة.
- تواتر قيمة لميزة إحصائية هو حاصل قسمة تكرارها على عدد أفراد المجتمع (أي التكرار الكلي).
- نسمي سلسلة إحصائية مجموعة القيم التي جمعت.
غالبا ما نمثل سلسلة إحصائية بجدول يشمل كل قيمة وتكرارها.
مثال:
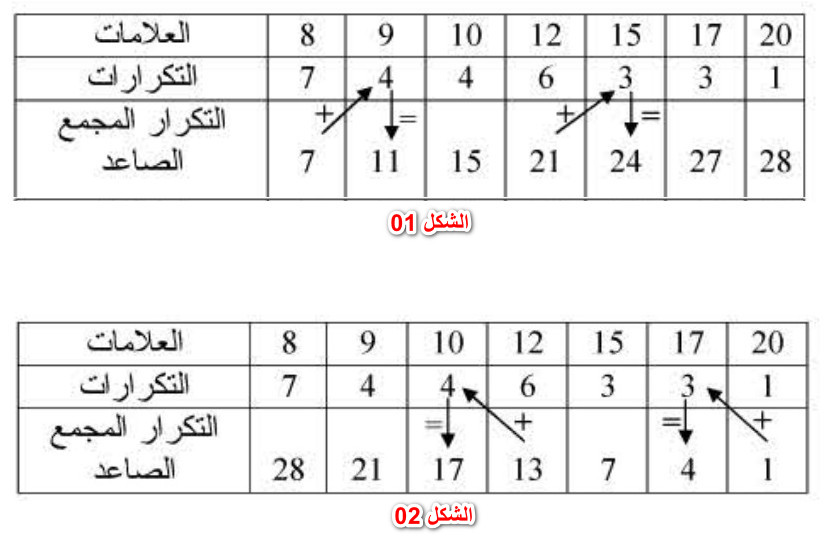
السلسلة الآتية تمثل علامات 28 تلميذا.
إليك جدول التكرارات والتواترات، التكرار الكلي هو: 28.
|
العلامات |
8 |
9 |
10 |
12 |
15 |
17 |
20 |
|
التكرارات |
7 |
4 |
4 |
6 |
3 |
3 |
1 |
|
التواترات |
|
|
|
|
|
|
|
التكرار المجمه المتزايد والمتناقص
2) التكرار المجمه المتزايد والمتناقص:
نفرض أن قيم الميزة مرتبة تصاعديا.
- التكرار المجمع المتزايد لقيمة (أو لفئة) هو مجموع تكرار هذه القيمة (أو الفئة) وتكرارات القيم (أو الفئات) الأصغر منها.
- التكرار المجمع المتناقص لقيمة (أو لفئة) هو مجموع تكرار هذه القيمة (أو الفئة) وتكرارات القيم (أو الفئات) الأكبر منها.
مثال (01):
باستعمال جدول التكرار السابق، ما هو التكرار المجمع الصاعد لكل قيمة؟
- لاحظ الشكل (01).
مثال (02):
باستعمال جدول التكرار السابق، ما هو التكرار المجمع التناقص لكل قيمة؟
- لاحظ الشكل (02).
التواتر المحمع المتزايد والمتناقص
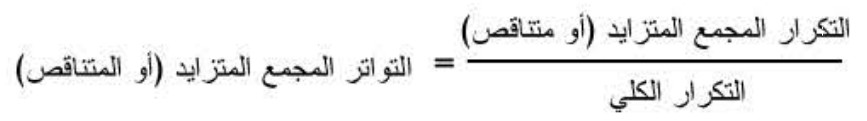
3) التواتر المحمع المتزايد والمتناقص:
- التواتر المجمع الصاعد (أو المتزايد) لقيمة (أو لفئة) هو مجموع تواتر هذه القيمة (أو الفئة) وتواترات القيم (أو الفئات) الأصغر منها.
- التواتر المجمع المتناقص (أو النازل) لقيمة (أو لفئة) هو مجموع توتر هذه القيمة (أو الفئة) وتوترات القيم (أو الفئات) الأكبر منها.
مثال:
في السلسلة المبينة في جدول التكرار الكلي هو:
|
القيم |
8 |
10 |
12 |
14 |
16 |
|
التكرارات |
4 |
6 |
5 |
2 |
3 |
|
التكرار م، ص |
4 |
10 |
(15) |
17 |
20 |
|
التكرار م، ن |
20 |
(16) |
10 |
5 |
3 |
- التواتر المجمع الصاعد للقيمة 8 هو: .
- التواتر المجمع الصاعد للقيمة 12 هو: .
- التواتر المجمع المتناقص للقيمة 10 هو: .
إذن:
التواتر المجمع المتزايد (أو المتناقص) يساوي التكرار المجمع المتزايد (أو المتناقص) على التكرار الكلي.
الوسيط الحسابي
4) الوسيط الحسابي:
تعريف:
إذا كانت : ،
،
...
قيم ميزة إحصائية وكانت :
،
،
...
تكراراتها على الترتيب فإن الوسط الحسابي
لهذه السلسلة الإحصائية يعطى بالعلاقة:
مثال:
إليك الجدول التكراري الآتي:
|
القيم |
8 |
10 |
12 |
15 |
|
التكرارات |
2 |
4 |
3 |
1 |
إيجاد الوسط الحسابي للسلسلة الإحصائية:
.
إذن: هو الوسط الحسابي للسلسلة الإحصائية.
الوسيط
5) الوسيط:
تعريف:
وسيط سلسلة إحصائية تكرارها الكلي هي القيمة التي تجزئها إلى جزئين لهما نفس التكرار، أي أن عدد القيم الأصغر من الوسيط يساوي عدد القيم الأكبر منه.
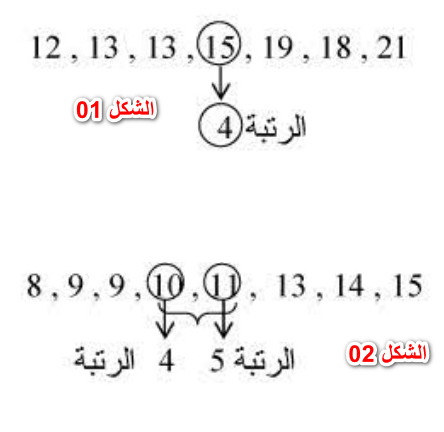
مثال (01):
أحسب وسيط السلسلة التالية المرتبة تصاعديا (لاحظ الشكل 01):
الحل:
بما أن عدد القيم للسلسلة الإحصائية هو فردي أي:
فإن رتبة الوسيط هي: إذن الوسيط هو
.
مثال (02):
أحسب وسيط السلسلة التالية المرتبة تصاعديا (لاحظ الشكل 02):
الحل:
بما أن عدد قيم السلسلة الإحصائية زوجي أي: .
فإن الوسيط هو المتوسط الحسابي للقيمتين اللتين تقعان في المرتبتين : و
.
إذن الوسيط هو:
المدى
6) المدى:
نعريف:
مدى سلسلة إحصائية هو الفرق بين أكبر قيمة وأصغر قيمة له.
مثال:
علامات علي هي : .
إذن مدى علامات علي هو: .